Type31-40.html

Type31-40.mws

> read `/Documents and Settings/ibuki/My Documents/ESC/ESC.mpl`;
ESC();

(1)

> with(algcurves):

TypeNo.31

> qc[31]:=x^4+x^3*z-y^2*z^2;

(1.1)

> with(plots):

with(algcurves):
plot_real_curve(subs(z=1,qc[31]),x,y);

Warning, the name changecoords has been redefined

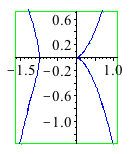Plot_2d

> singularities(subs(z=1,qc[31]),x,y);

(1.2)

> subs(y=t*(x+z)+z,qc[31]);

(1.3)

> Q31:=mapfactor(subs({z=1,x=U},%),U);

(1.4)

> subs(U=-1,Q31);
simplify(%);

(1.5)

> Quartic_to_Weierstrass(Q31,[-1,I]);

(1.6)

> step5(%[1],{x=X,z=Z,y=Y},{x,y,z});

(1.7)

> mapfactor(subs({X=4*X,Y=8*Y},%[1])/64,[X,Y]);

(1.8)

> Elliptic_surface(%);

(1.9)

> Show_data();

(1.10)

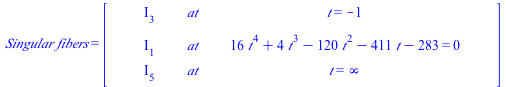Typesetting:-mrow(Typesetting:-mrow(Typesetting:-mi( (1.10)

(1.10)

> latex(y^2 = x^3+(t^2-3)*x^2+(6*t+7)*x-4-4*t);

{y}^{2}={x}^{3}+ \left( {t}^{2}-3 \right) {x}^{2}+ \left( 6\,t+7

\right) x-4-4\,t

TypeNo.32

> qc[32]:=x^4+x^3*z-y^2*z^2;

(2.1)

> with(plots):

with(algcurves):
plot_real_curve(subs(z=1,qc[32]),x,y);

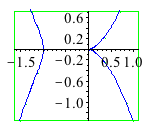Plot_2d

> singularities(subs(z=1,qc[32]),x,y);

(2.2)

> subs(z=t*(x-y),qc[32]);

(2.3)

> Q32:=mapfactor(subs({y=1,x=U},%),U);

(2.4)

> subs(U=1,Q32);
simplify(%);

(2.5)

> Quartic_to_Weierstrass(Q32,[1,1]);

(2.6)

> step5(%[1],{x=X,z=Z,y=Y},{x,y,z});

(2.7)

> mapfactor(subs({X=4*X,Y=8*Y},%[1])/64,[X,Y]);

(2.8)

> Elliptic_surface(%);

(2.9)

> Show_data();

(2.10)

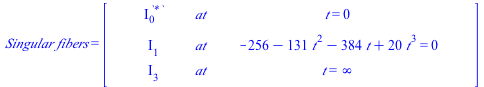Typesetting:-mrow(Typesetting:-mrow(Typesetting:-mi( (2.10)

(2.10)

TypeNo.33

> qc[33]:=-y^2*(3*x^2-(3*z-y)^2)+x^3*(9*x+2*y-12*z);

(3.1)

> with(plots):

with(algcurves):
plot_real_curve(subs(z=1,qc[33]),x,y);

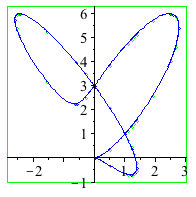Plot_2d

> singularities(subs(z=1,qc[33]),x,y);

(3.2)

> subs(y=t*x+6*z,qc[33]);

(3.3)

> Q33:=mapfactor(subs({z=1,x=U},%),U);

(3.4)

> subs(U=0,Q33);
simplify(%);

(3.5)

> Quartic_to_Weierstrass(Q33,[0,18]);

(3.6)

(3.7)

> step5(%[1],{x=X,z=Z,y=Y},{x,y,z});

(3.8)

> mapfactor(subs({X=4*9*X,Y=8*27*Y},%[1])/(64*729),[X,Y]);

(3.9)

> mapfactor(subs({X=9*X,Y=27*Y},%)/729,[X,Y]);

(3.10)

> mapfactor(subs({X=9*X,Y=27*Y},%)/729,[X,Y]);

(3.11)

> Elliptic_surface(%);

(3.12)

> Show_data();

(3.13)

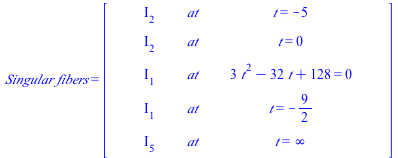Typesetting:-mrow(Typesetting:-mrow(Typesetting:-mi( (3.13)

(3.13)

TypeNo.34

> qc[34]:=x^4+y^4-x^2*z^2;

(4.1)

> with(plots):

with(algcurves):
plot_real_curve(subs(z=1,qc[34]),x,y);

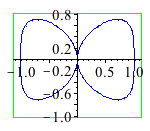Plot_2d

> singularities(subs(z=1,qc[34]),x,y);

(4.2)

> subs(z=t*x,qc[34]);

(4.3)

> Q34:=mapfactor(subs({y=1,x=U},%),U);

(4.4)

> subs(U=0,Q34);
simplify(%);

(4.5)

> Quartic_to_Weierstrass(Q34,[0,1]);

$`+`(`*`(`^`(Y, 2), `*`(Z)), `-`(`*`(`^`(X, 3))), `-`(`*`(4, `*`(`+`(t, `-`(1)), `*`(`+`(t, 1), `*`(X, `*`(`^`(Z, 2)))))))), {X = `+`(`*`(2, `*`(`+`(V, 1), `*`(U)))), Y = `+`(`*`(4, `*`(V)), 4), Z = `*...$
$`+`(`*`(`^`(Y, 2), `*`(Z)), `-`(`*`(`^`(X, 3))), `-`(`*`(4, `*`(`+`(t, `-`(1)), `*`(`+`(t, 1), `*`(X, `*`(`^`(Z, 2)))))))), {X = `+`(`*`(2, `*`(`+`(V, 1), `*`(U)))), Y = `+`(`*`(4, `*`(V)), 4), Z = `*...$ (4.6)

> step5(%[1],{x=X,z=Z,y=Y},{x,y,z});

$`+`(`*`(`^`(Y, 2), `*`(Z)), `-`(`*`(`^`(X, 3))), `-`(`*`(4, `*`(`+`(t, `-`(1)), `*`(`+`(t, 1), `*`(X, `*`(`^`(Z, 2)))))))), {x = X, y = Y, z = Z}, [x, y, z]$ (4.7)

> mapfactor(subs({X=X,Y=Y},%[1]),[X,Y]);

(4.8)

> Elliptic_surface(%);

(4.9)

> Show_data();

(4.10)

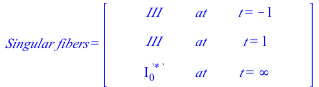Typesetting:-mrow(Typesetting:-mrow(Typesetting:-mi( (4.10)

(4.10)

TypeNo.35

> qc[35]:=(x^2+y^2-z^2)*(2*x^2+y^2-2*z^2);

(5.1)

> with(plots):

with(algcurves):
plot_real_curve(subs(z=1,qc[35]),x,y);

Warning, the name changecoords has been redefined

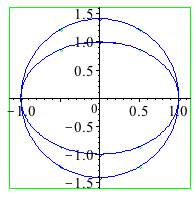Plot_2d

> singularities(subs(z=1,qc[35]),x,y);

(5.2)

> subs(y=t*x+2*z,qc[35]);

(5.3)

> Q35:=mapfactor(subs({z=1,x=U},%),U);

(5.4)

> subs(U=0,Q35);
simplify(%);

(5.5)

> Quartic_to_Weierstrass(Q35,[0,6^(1/2)]);

(5.6)

> step5(%[1],{x=X,z=Z,y=Y},{x,y,z});

(5.7)

> mapfactor(subs({X=X,Y=Y},%[1]),[X,Y]);

(5.8)

> Elliptic_surface(%);

(5.9)

> Show_data();

(5.10)

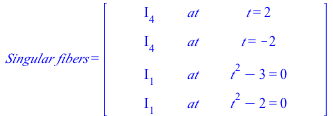Typesetting:-mrow(Typesetting:-mrow(Typesetting:-mi( (5.10)

(5.10)

TypeNo.36

> qc[36]:=x^4+x^3*z+y^2*z^2;

(6.1)

> with(plots):

with(algcurves):
plot_real_curve(subs(z=1,qc[36]),x,y);

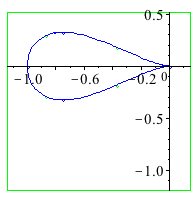Plot_2d

> singularities(subs(z=1,qc[36]),x,y);

(6.2)

> subs(z=t*(x-2*y)+2*y,qc[36]);

(6.3)

> Q36:=mapfactor(subs({y=1,x=U},%),U);

(6.4)

> subs(U=2,Q36);
simplify(%);

(6.5)

> Quartic_to_Weierstrass(Q36,[2,6]);

(6.6)

> step5(%[1],{x=X,z=Z,y=Y},{x,y,z});

(6.7)

> mapfactor(subs({X=4*9*X,Y=8*27*Y},%[1])/(729*64),[X,Y]);

(6.8)

> Elliptic_surface(%);

(6.9)

> Show_data();

(6.10)

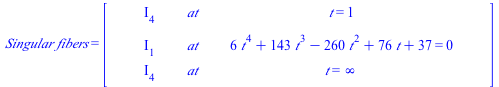Typesetting:-mrow(Typesetting:-mrow(Typesetting:-mi( (6.10)

(6.10)

TypeNo.37

> qc[37]:=x^4+x^3*z-2*y^2*z^2;

(7.1)

> with(plots):

with(algcurves):
plot_real_curve(subs(z=1,qc[37]),x,y);

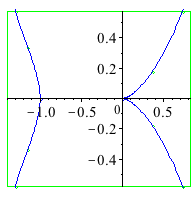Plot_2d

> singularities(subs(z=1,qc[37]),x,y);

(7.2)

> subs(y=t*(x-z)+z,qc[37]);

(7.3)

> Q37:=mapfactor(subs({z=1,x=U},%),U);

(7.4)

> subs(U=1,Q37);
simplify(%);

(7.5)

> Quartic_to_Weierstrass(Q37,[1,0]);

(7.6)

> step5(%[1],{x=X,z=Z,y=Y},{x,y,z});

(7.7)

> mapfactor(subs({X=X,Y=Y},%[1]),[X,Y]);

(7.8)

> Elliptic_surface(%);

(7.9)

> Show_data();

(7.10)

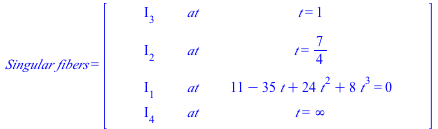Typesetting:-mrow(Typesetting:-mrow(Typesetting:-mi( (7.10)

(7.10)

TypeNo.38

> qc[38]:=(x^2+y^2)^2-x^2*z^2+y^2*z^2;

(8.1)

> with(plots):

with(algcurves):
plot_real_curve(subs(z=1,qc[38]),x,y);

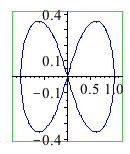Plot_2d

> singularities(subs(z=1,qc[38]),x,y);

${[[0, 0, 1], 2, 1, 2], [[RootOf(`+`(`*`(`^`(_Z, 2)), 1)), 1, 0], 2, 1, 2]}$ (8.2)

> subs(z=t*x,qc[38]);

(8.3)

> Q38:=mapfactor(subs({y=1,x=U},%),U);

(8.4)

> subs(U=0,Q38);
simplify(%);

(8.5)

> Quartic_to_Weierstrass(Q38,[0,1]);

(8.6)

(8.7)

> step5(%[1],{x=X,z=Z,y=Y},{x,y,z});

(8.8)

> mapfactor(subs({X=X,Y=Y},%[1]),[X,Y]);

(8.9)

> Elliptic_surface(%);

(8.10)

> Show_data();

(8.11)

Typesetting:-mrow(Typesetting:-mrow(Typesetting:-mi( (8.11)

(8.11)

TypeNo.39

> qc[39]:=(x^2+y^2-x*z)^2-x^2*z^2-y^2*z^2;

(9.1)

> with(plots):

with(algcurves):
plot_real_curve(subs(z=1,qc[39]),x,y);

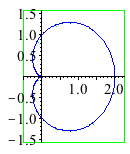Plot_2d

> singularities(subs(z=1,qc[39]),x,y);

${[[0, 0, 1], 2, 1, 1], [[RootOf(`+`(`*`(`^`(_Z, 2)), 1)), 1, 0], 2, 1, 1]}$ (9.2)

> subs(y=t*(x-z),qc[39]);

(9.3)

> Q39:=mapfactor(subs({z=1,x=U},%),U);

(9.4)

> subs(U=1,Q39);
simplify(%);

(9.5)

> Quartic_to_Weierstrass(Q39,[1,I]);

(9.6)

(9.7)

> step5(%[1],{x=X,z=Z,y=Y},{x,y,z});

(9.8)

> mapfactor(subs({X=X,Y=Y},%[1]),[X,Y]);

(9.9)

> Elliptic_surface(%);

(9.10)

> Show_data();

(9.11)

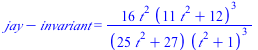`+`(jay, `-`(invariant)) = `+`(`/`(`*`(16, `*`(`^`(t, 2), `*`(`^`(`+`(`*`(11, `*`(`^`(t, 2))), 12), 3)))), `*`(`+`(`*`(25, `*`(`^`(t, 2))), 27), `*`(`^`(`+`(`*`(`^`(t, 2)), 1), 3))))) (9.11)

(9.11)

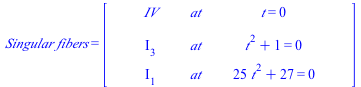Typesetting:-mrow(Typesetting:-mrow(Typesetting:-mi( (9.11)

(9.11)

TypeNo.40

> qc[40]:=(x^2+y^2-2*x*z)^2-x^2*z^2-y^2*z^2;

(10.1)

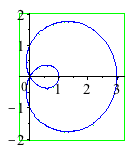
> with(plots):

with(algcurves):
plot_real_curve(subs(z=1,qc[40]),x,y);

Plot_2d

> singularities(subs(z=1,qc[40]),x,y);

${[[0, 0, 1], 2, 1, 2], [[RootOf(`+`(`*`(`^`(_Z, 2)), 1)), 1, 0], 2, 1, 1]}$ (10.2)

> subs(y=t*x+z,qc[40]);

(10.3)

> Q40:=mapfactor(subs({z=1,x=U},%),U);

(10.4)

> subs(U=0,Q40);
simplify(%);

(10.5)

> Quartic_to_Weierstrass(Q40,[0,0]);

(10.6)

(10.7)

> step5(%[1],{x=X,z=Z,y=Y},{x,y,z});

(10.8)

> mapfactor(subs({X=X,Y=Y},%[1]),[X,Y]);

(10.9)

> Elliptic_surface(%);

(10.10)

> Show_data();

(10.11)

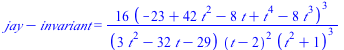`+`(jay, `-`(invariant)) = `+`(`/`(`*`(16, `*`(`^`(`+`(`-`(23), `*`(42, `*`(`^`(t, 2))), `-`(`*`(8, `*`(t))), `*`(`^`(t, 4)), `-`(`*`(8, `*`(`^`(t, 3))))), 3))), `*`(`+`(`*`(3, `*`(`^`(t, 2))), `-`(`*... (10.11)

(10.11)

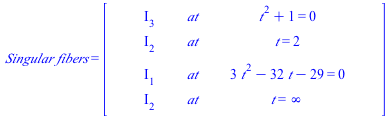Typesetting:-mrow(Typesetting:-mrow(Typesetting:-mi( (10.11)

(10.11)